Basic Stuff About Vectors
1. Vectors and Vector Algebraic Operations
A scalar is a quantity that can be defined by a number
alone. A vector, on the other hand, must be specified by both a number
and a direction. From a geometric point of view, a vector can be defined
as a line segment having a specific direction and a specific length. The
symbol for a vector normally will be a boldfaced letter with an arrow overhead.
In this document, however, in order to make documents on the web easier
to construct, a simple boldface letter will be used. i.e., A. The
length of the vector is its magnitude and is written as |A| or when
unambiguous, as the letter itself in italics, i.e., A.
Vectors follow an algebra that is motivated by their applications,
and we shall use them often. These algebraic operations are described in
your book, but they include:
rule 1 - There exists a zero vector.
rule 2 - A vector A multiplied by a scalar m
is a vector, unchanged in direction, but
modified in length by the factor m.
rule 3 - The negative of a vector is the original vector
flipped 180 degrees;.
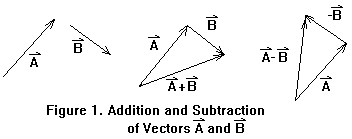
rule 4 - Two vectors, A and B, are added
by placing the tail of one on the head of
the other (in either order) and defining the sum to
be the vector drawn
from the tail of the first to the head of the second.
rule 5 - A vector B can be subtracted from a vector
A
by adding -B to A.
In addition to these rules, two different ways to multiply
vectors are useful. The first is the scalar or dot product
of vectors A and B and is defined to result in a scalar having
the value
A dot B = |A||B| cos(alpha)
where alpha is the angle between
A and B.
Why is this operation defined this way? The reason is that it turns out
to be useful in describing certain physical quantities-work, for example.
The second way to multiply vectors is designed to result in a vector. The
vector
or
cross
product is defined to have the magnitude
|A cross B|=|A||B| sin(alpha)
where alpha is again the angle between the two vectors
(the smaller of the two possible angles). The vector product is useful
in describing rotational motion, for example. Unlike the dot product, the
vector product is a vector. The direction of the vector (A crossB)
is defined by the so-called right-hand rule. Using the fingers of the right
hand pointed in the direction of A, the fingers are rotated into
the vector B(remember - the smaller of the two possible angles).
The vector (A cross B) is then perpendicular to both A
and B and points in the direction of one's thumb. A vector dotted
into itself gives the square of the length of the vector. Thus A
dot A = A2.
We also see that if A is perpendicular to B, then A
dot B = 0. In contrast, a vector crossed into itself (A cross
A)
is 0. By the right-hand rule, although the scalar product commutes, the
vector product does not. That is to say, although A dot B
=
B
dot A, (A cross B) does not equal (Bcross
A). Instead, (A cross B) = - (Bcross
A).In this discussion we concentrate on the operations
of addition and subtraction. The operation of scalar and vector multiplication
will be discussed later in the course, but only to the extent that they
are needed.
2. Vectors and Rectangular Coordinates
The first skill we need is adding (or subtracting) vectors
algebraically. To this end, the concept of vector components gives us the
tools required. A vector is a pure entity, an arrow if we wish, independent
of any particular coordinate system. But once we introduce coordinates,
we can specifically describe the vector as it appears in that system.
For simplicity, let us assume a two-dimensional rectangular system defined
by x and y axes. Then the vector can be determined if we
know its length and the angle made with respect to the x
axis. Alternatively, the vector is completely determined if we know its
components
along both the x and y axes, respectively. For a vector A,
which has a length A and makes an angle alpha with respect to the
x
axis, the components are called Ax and Ay.
They are defined as the projection of the vector along each axis. The location
of the vector is not of significance. All vectors having the same length
and same orientation in a given x-y coordinate system have
the same components and are equivalent to each other.
Ax = A cos(alpha) ;
Ay = A sin(alpha)
In summary, we completely specify the vector either
by writing A in terms of (A, alpha ) or A in terms
of (Ax, Ay).
Looking back to Fig. 1, we can draw on the figure any
rectangular system whatsoever, then calculate the components of the vectors
A
and B separately in the system we have drawn. Then, knowing the
components of A and B separately, we automatically also know
the components of the sum C = A + B in the same system, because
Cx = Ax + Bx
and Cy = Ay + By.
The algebra of adding and subtracting vectors becomes
clear. We choose a coordinate system, calculate the components in that
system and add and subtract the components!
Activity 1: The vectors A and
B are defined as A = (5,37°) and B = (10,53°
) in a
particular x-y coordinate system. (Assume 37°
, 90° and 53°
defines a 3-4-5 triangle.)
a) Find each vector in component form in the same x-y system.
b) Find the components of the vectors C = A + B and D = A - B.
c) Use trig to find the vectors C and D in the (magnitude, angle)
notation.
3. Extension to Three Dimensions; Base Vectors in Cartesian
Coordinates
When describing motion, solutions to many problems become
simple if the right coordinate system is chosen. Sometimes, the right coordinate
system is rectangular; sometimes a better choice might be polar or cylindrical
or even spherical polar. We will mainly deal with the rectangular or cartesian
system, in which the x-y-z axes are all orthogonal (orthogonal means
perpendicular) to each other and in the order shown in Figure 2. In this
system we draw at the point P(x,y,z) in space a vector A
with its three components AxAy
and Az, referred to the
coordinate system. 
As in the two-dimensional case, this vector is completely
specified once we know its components along each of the three axes. In
order to express A in terms of the chosen coordinate system, we
need to write it in such a a way that its vector nature is clear. Toward
this goal, we define three unit vectors (vectors with a magnitude
of 1), each parallel to one of the three axes. In our x-y-z system
these unit vectors are i, j and k and are parallel to x,
y
and z, respectively. Now, if the unit vector i is multiplied
by the scalar Ax, then Axi is a vector of length Ax
and directed parallel to the x axis. As a consequence,
A
can be written
A = Ax i + Ay
j + Az k,
This is handy notation, knowing that adding and subtracting
vectors is done using components. The notation gives us an algebraic form
in which to express a variety of vector operations. Thus, for example,
the difference between two vectors, A and B can be expressed
as B - A = (Bx - Ax) i + (By
- Ay) j + (Bz - Az)
k. For many problems, the full three dimensions may not be needed
because the motion is confined to a plane. In this case, the common practice
is to use x and y, eliminating z.
As discussed earlier, a general vector describes a physical
quantity at a point in space and does not depend on any coordinate system.
Coordinate axes can be placed anywhere and with any orientation. When described
in terms of different cartesian systems, a given vector may have different
looking components, but the length and orientation of the vector remain
the same.
Activity 2: Refer back to Activity 1 and express
all results in unit vector notation.
Activity 3: (Small Challenge): Given the
vector G = i + 2j + k, use trigonometry to
find the length of the vector and the angle the vector makes with
respect to the x axis.
4. The Position Vector in Cartesian Coordinates
Let us assume that we want to describe the position
of an object as it moves through space along a path described by the function
P(x,y,z).
We use a rectangular system as before, with orthogonal x-y-z axes.
In this coordinate system we draw a special kind of vector called a position
vector, with the tail at the origin and the head at the position P(x,y,z).
This vector, labeled R in Figure 3, is completely specified by giving
the components along each axis.  In
order to express R in terms of the chosen coordinate system, we
use the three unit vectors i, j and k. As a consequence,
R
is
In
order to express R in terms of the chosen coordinate system, we
use the three unit vectors i, j and k. As a consequence,
R
is
R = Rx i + Ry
j + Rz k º x
i + y j + z k,
As the object moves through space, the position vector
traces a path. Let us assume that the value of R at two different
times is known. The difference between these two position vectors is
R2 - R1
= delta R = (x2
- x1)
i + (y2
- y1)
j + (z2
- z1) k.
This last expression is a vector that goes from (x1,
y1, z1)
to (x2, y2,
z2)
and is exactly like the vectors A or B discussed in Section
4. An important difference between a position vector R and a
general vector such as delta R is that the components of R
are x, y and z, whereas for delta R the components
are delta x, delta y and delta z. It is important
to distinguish between true vectors and position vectors. A true vector
does not depend on coordinate system but only on the difference between
one end of the vector and the other. A position vector, in contrast, does
depend on the coordinate system, because it is used to locate a position
relative to a specified reference point.
Some of the previous discussion may feel abstract to you.
Do not worry about that because you gradually will become comfortable with
the ideas as you use them and as you see then used in lectures. Vector
notation is simply a short-hand way of expressing information in a compact
but precise way.
Answers to Activities
1. a) Ax = 4, Ay = 3,
Bx
= 6, By = 8
b) Cx = 10, Cy = 11,
Dx
= -2, Dy = -5
c) C = (14.9,48°
), D = (5.4,-68° )
2. A = 4 i + 3 j, B = 6 i
+ 8 j, C = 10 i + 11 j, D = - 2 i
- 5 j
3. The squared length of the vector is G2
= 12 + 22 + 12. Thus, L = sqrt
6.
The angle between the vector and the x axis is
the angle whose cosine is Gx/G.
This angle is 66° .


 In
order to express R in terms of the chosen coordinate system, we
use the three unit vectors i, j and k. As a consequence,
R
is
In
order to express R in terms of the chosen coordinate system, we
use the three unit vectors i, j and k. As a consequence,
R
is